Creating black holes in materials !
May.10 2017
A material that mimics the behavior of a black hole is developed by researchers in China and Singapore. Yugui Yao from the Beijing Institute of Technology and colleagues show that mechanical strain in a material known as Dirac semimetal can imitate the warping of space–time predicted by general relativity. Simulations of the Universe predict a wide range of counter-intuitive phenomenon. But many of these are beyond state-of-the-art technology to detect. Instead, scientists can engineer materials that are governed by equations similar to those that define astrophysical phenomena. Yao et al. investigate Dirac semimetals whose electronic bandstructure gives rise to massless quasiparticles that resemble relativistic particles. They show that altering the uniaxial strain enables control over these quasiparticles so that they emulate the behavior associated with black and white holes, event horizons and gravitational lensing.
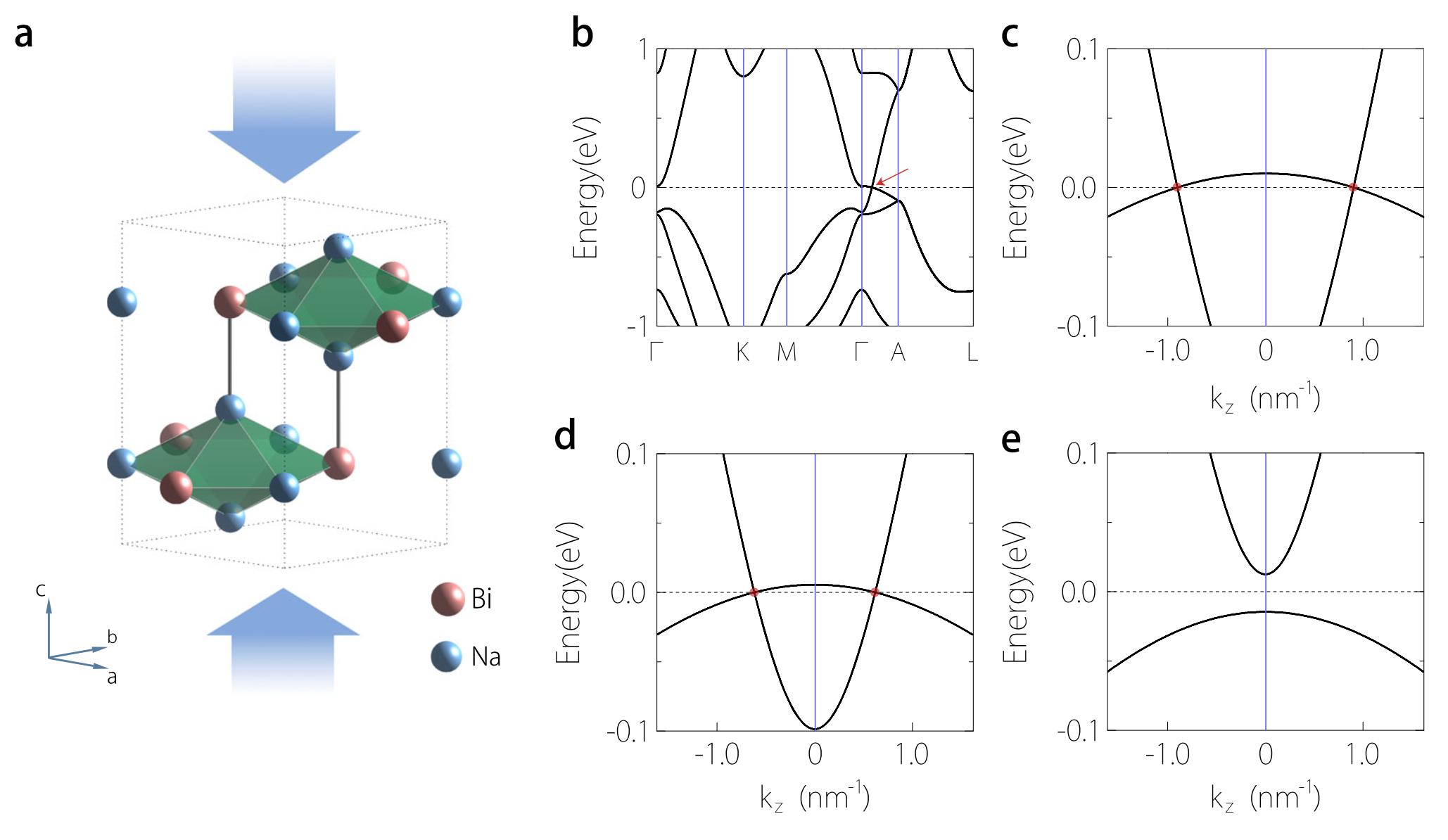
Figure 1 First-principles band structure results for Na3Bi. a Schematic representation of Na3Bi lattice structure under uniaxial strain. b Band structure without strain. c–e Enlarged band structures near the Γ point along the k z-axis for strain value c 0%, d −3%, and e −7%. The Dirac points are indicated by the red arrow in b and by red dots in c, d
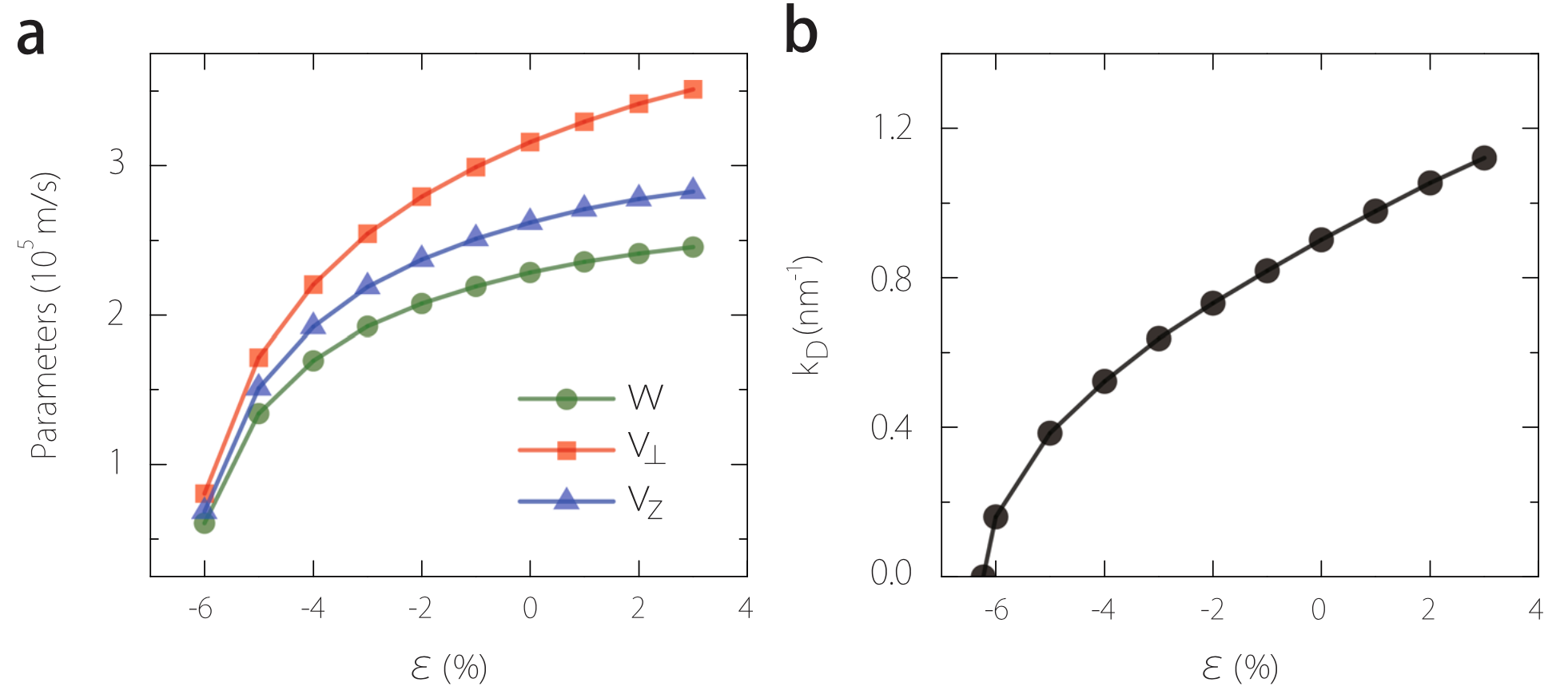
Figure 2 Model parameter vs. strain. The model parameters a v⊥, vz, w, and b kD in Eq. (3) as a function of strain obtained by fitting the first-principles band structures of Na3Bi
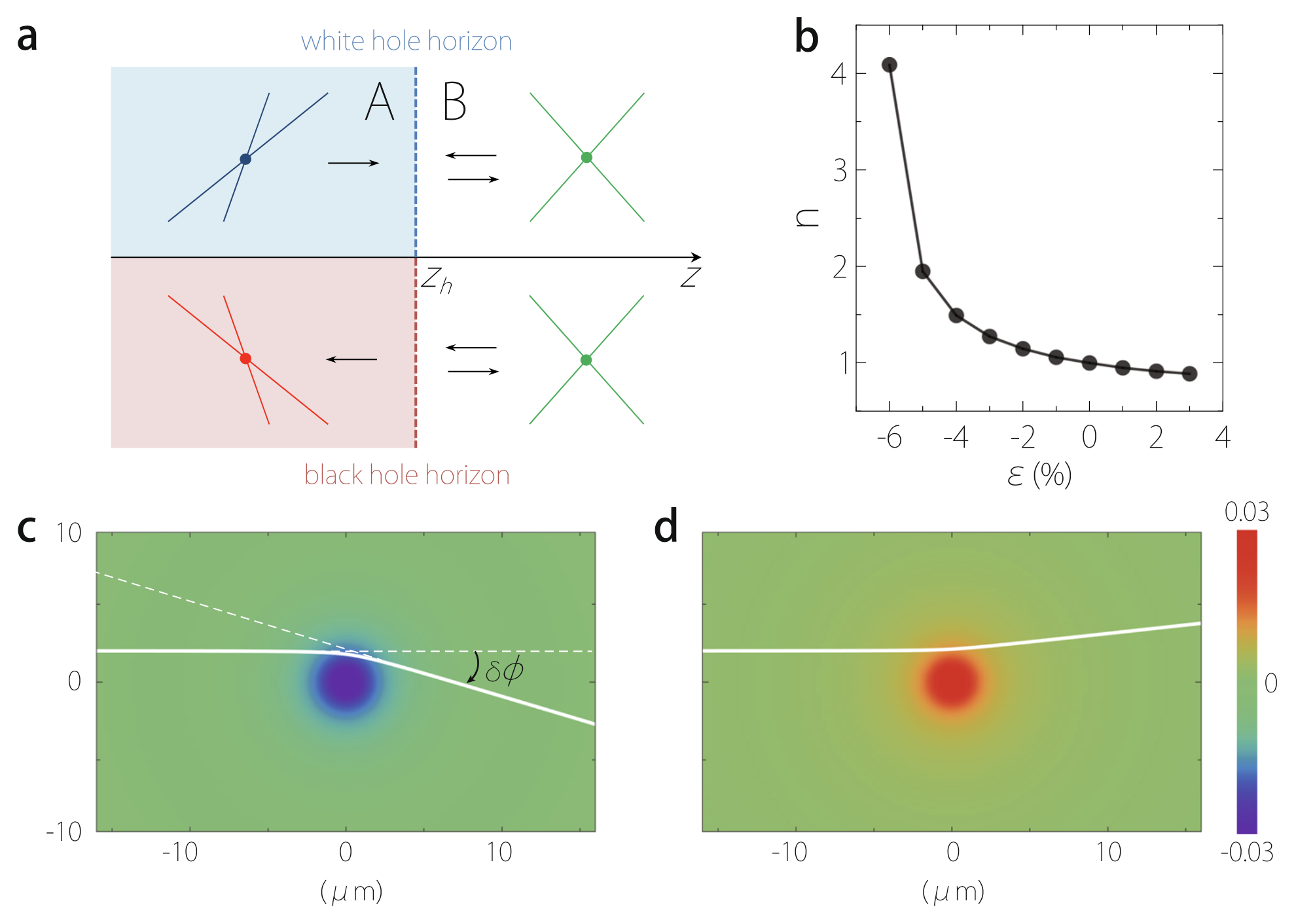
Figure 3 Astrophysical analogues in strained topological semimetal. a Schematic figure showing (up) a white-hole horizon and (bottom) a black-hole horizon at z = z h, corresponding to the Schwarzschild radius of metric (5). The arrows indicate the quasiparticle propagation directions in each region. b Effective refractive index n for quasiparticle propagation vs. strain. c,d Analogue of gravitational lensing effect. The white line indicates a quasiparticle trajectory (geodesic) in the xy-plane. δϕ indicates the deflection angle. The colormap shows the strain profile. In b–d, parameters of Na3Bi are used
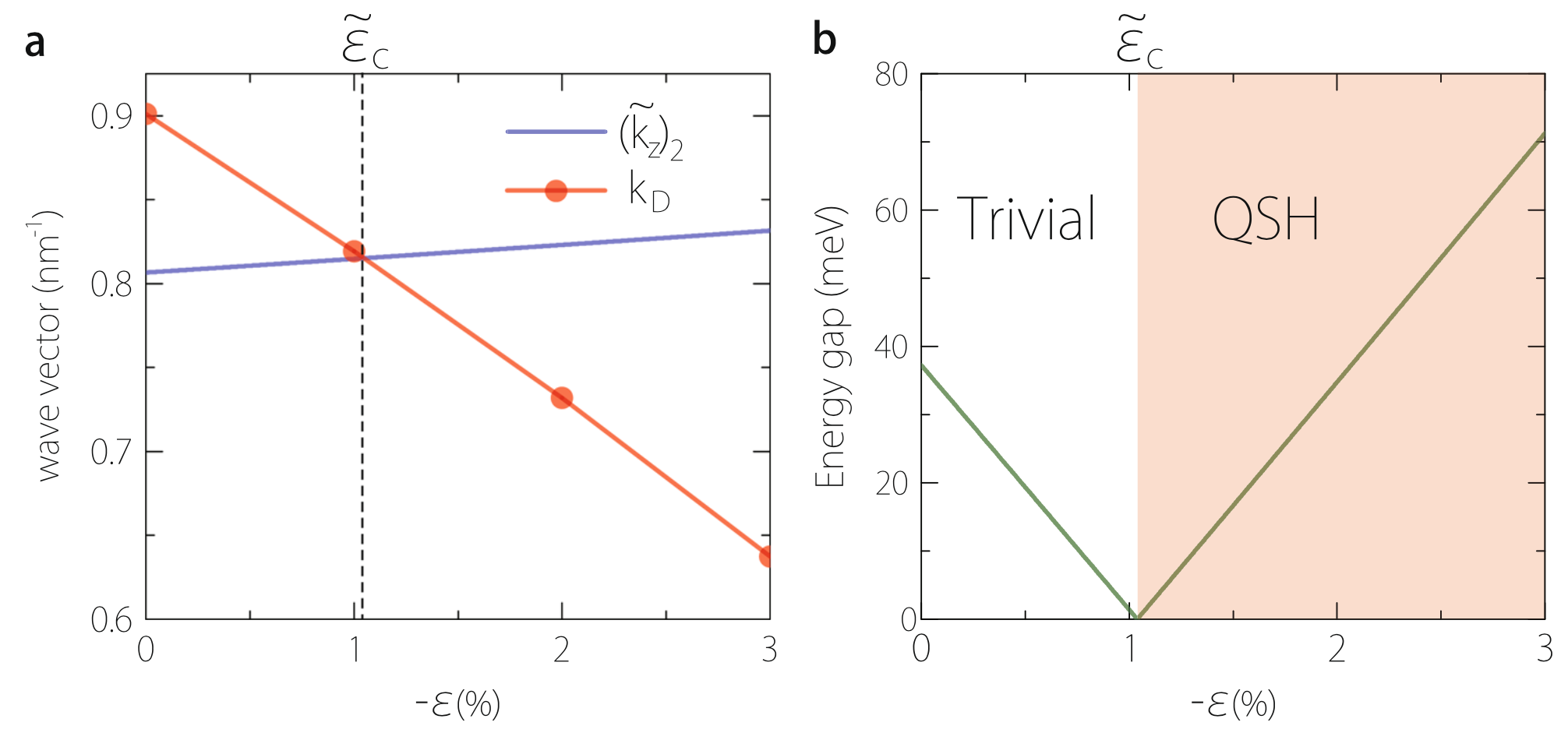
Figure 4 Topological phase transition in thin film. a The quantum well effective wave-vector (for the second quantum well subband) and kD vs. strain. Their crossing-point at critical strain marks a topological phase transition between a trivial insulating and a QSH insulating phases. The corresponding subband gap closes at , as shown in b. Here we take a Na3Bi thin film with 16-layer thickness (≈78 Å)
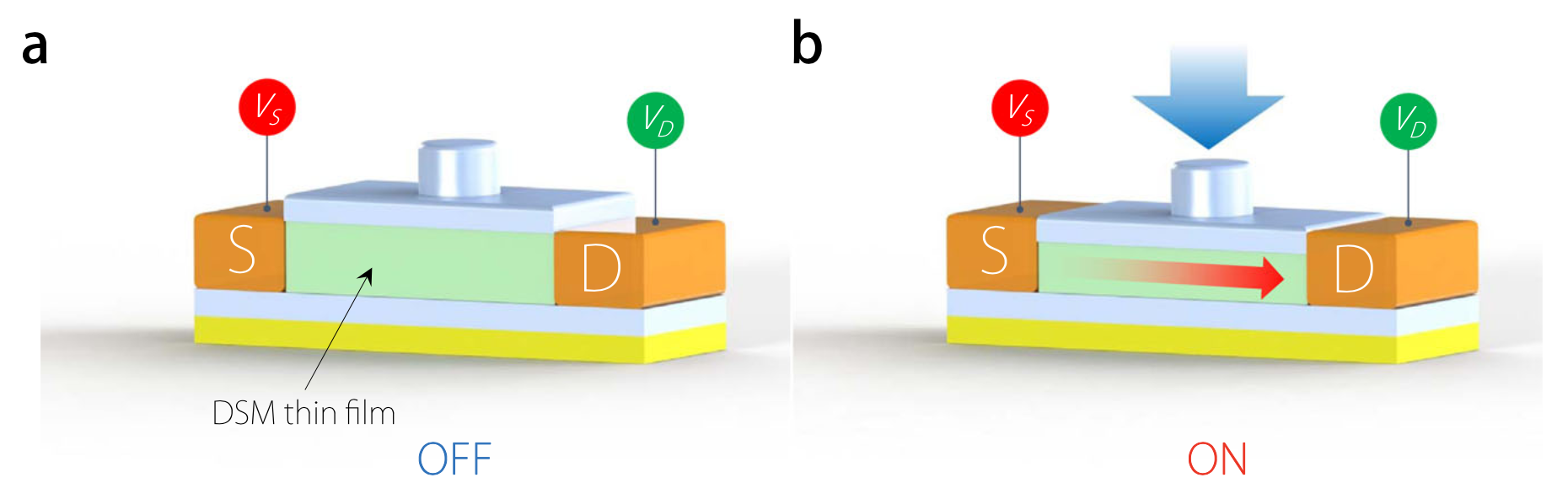
Figure 5 Piezo-topological transistor.Schematic of a piezo-topological transistor using DSM thin film as the channel material. a The thin film is initially in the trivial insulating phase, so the transistor is in off state. b By applying strain to the channel region, the thin film is driven to the QSH phase with topological edge channels for conducting current. Hence the transistor is turned on. The topological channels are robust and have low heat dissipation
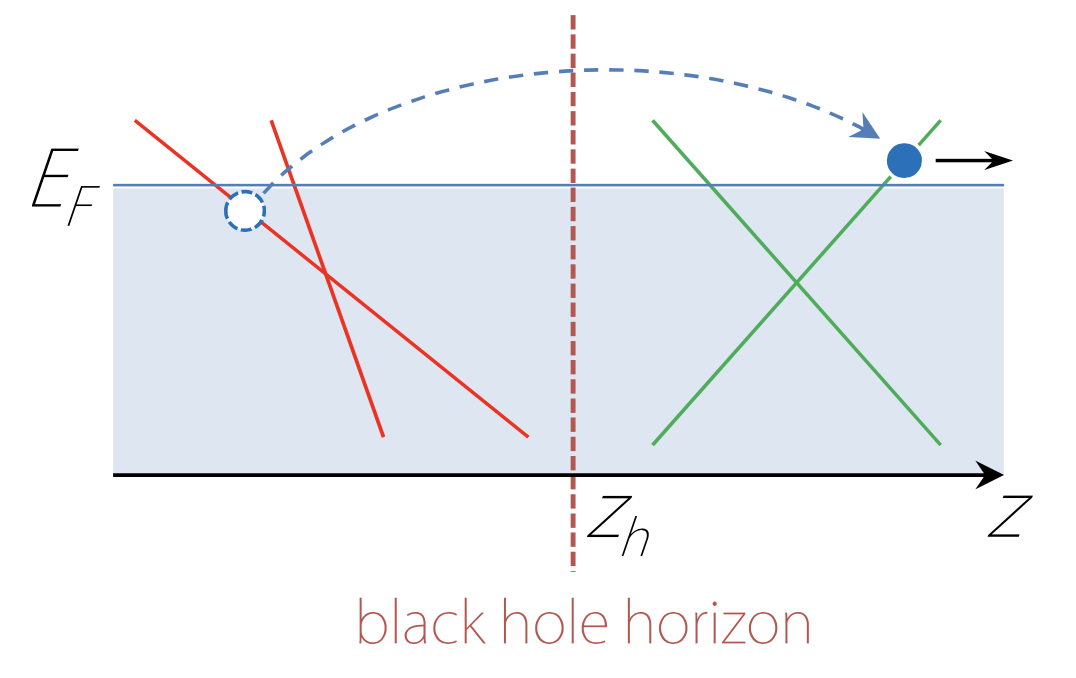
Figure 6 Analogue of Hawking radiation. Illustration of the analogue of Hawking radiation in a topological semimetal. A tunneling process due to quantum fluctuation near an artificial black-hole horizon leads to the creation of quasipartile outside the Horizon and a quasihole inside the horizon. The quasiparticle escapes from the horizon, resembling the Hawking radiation. Here EF indicates the Fermi energy